Zadání posledního - čtvrtého - kola soutěže NEŘEŠ
Autor: Sranda žabky <->, Téma: _Matematika, Vydáno dne: 14. 06. 2012Jedete příští týden na výlet? Vezměte si s sebou zadání NEŘEŠ!
Pro želvy jsme tentokrát vymysleli specialitu - bonusová šifra, na kterou jen tak nepřijdete.
NEŘEŠ – 4. kolo, 5.6. – 25.6. 2012 Želvy
Motto: Nikdy jsem nedopustil, aby škola stála v cestě mému vzdělání. Mark Twain
1) Najděte všechny dvojice celých čísel x, y, které splňují následující rovnici:
(-1)(x – y + x•y + 1) = (-1)(x + y – x•(y + 1))
2) Jsou dány tři kružnice, které mají každá s každou vnější dotyk. Po spojení středů kružnic vznikne trojúhelník. Vypočtěte obsah vyšrafované části, jestliže víte, že poloměry kružnic mají hodnoty 4, 6, 9. (V šifře najdete nápovědu, jak příklad řešit.)
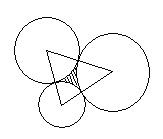
ŠIFRA(ZA VYŘEŠENÍ 3 BODY NAVÍC): 3 5 1 6 5 9 4 10 4 2 3 1
3) Každý špaččí pár má 16 potomků. Každý pár těchto potomků má opět 16 potomků atd. Předpokládejme, že jedna generace trvá tři měsíce a že špačci neumřou dokud nemají všech 16 potomků. Jak dlouho bude trvat, než bude mít populace špačků stejnou hmotnost jako Slunce, jestliže předpokládáme, že jeden špaček váží 100g?
NEŘEŠ – 4. kolo, 5.6. – 25.6. 2012 Svišti
Motto: Co slyším, to zapomenu. Co vidím, si pamatuji. Co si vyzkouším, tomu rozumím. Konfucius
1) Věřitel jedoucí tramvají zpozoroval svého dlužníka jdoucího podél kolejí opačným směrem, než jela tramvaj. Během deseti sekund se věřitel dostal k východu, vyskočil z tramvaje a běžel, aby dlužníka dohonil. Věřitel běžel dvakrát rychleji než dlužník, ale pětkrát pomaleji, než jela tramvaj. Po jaké době dlužníka dohonil?
2) Ze čtvercového plechu o straně 24 cm máme vyrobit krabici (bez víka) se čtvercovým dnem a s celočíselnými rozměry. Jaký největší objem může mít krabice?
3) Ciferník hodin rozdělte jednou čarou tak, aby čísla ležící ve stejných částech ciferníku měla stejný součet. Lze ciferník rozdělit více čarami, aby vznikly tři stejné součty nebo šest stejných součtů?